Transverse Universelle de Mercator
Ouvrir le menu principal
Rechercher
Photographiez votre culture locale, aidez Wikipédia et gagnez des prix !
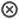
Transverse universelle de Mercator
La projection Transverse universelle de Mercator (en anglais Universal Transverse Mercator ou UTM) est un type de projection cartographique conforme de la surface de la Terre. L’Allemagne l’utilise sous le nom de Projection de Gauss-Krüger. Cette projection est une projection cylindrique transverse où l’axe du cylindre croise perpendiculairement l’axe des pôles de l’ellipsoïde terrestre au centre de l’ellipsoïde.
Schéma de la projection UTM
Elle s'appuie sur le même principe de déformation que la projection de Mercator classique mais la trame en jeu (celle qui va se transformer en un quadrillage) n'est plus constituée des méridiens et des parallèles qui, eux, sont transformés en lignes courbes. La trame d'une transverse de Mercator est constituée des grands cercles possédant l'axe du cylindre comme axe de symétrie et des petits cercles possédant l'axe du cylindre comme axe de rotation.
Illustration du principe de la projection transverse de Mercator pour 18 projections de fuseaux de 20° (au lieu de 60 projections de fuseaux de 6°)
En pratique, pour couvrir la surface de la Terre, on la découpe en 60 fuseaux de 6 degrés en séparant l’hémisphère Nord et l’hémisphère Sud. Soit au total 120 zones (60 pour le Nord et 60 pour le Sud) et donc 60 projections transverses différentes. On développe alors le cylindre tangent à l’ellipsoïde le long d’un méridien pour obtenir une représentation plane.
Les zones polaires (au-delà de 84,5 degrés de latitude Nord et en deçà de 80,5 degrés de latitude Sud) ne sont théoriquement pas couvertes par ce système de projection, bien que le cylindre utilisé soit tangent aux deux pôles.
Ce n’est cependant pas un réel obstacle, si on admet d’étendre le découpage rectangulaire de la projection, de façon à couvrir plus de 6° de longitudes au-delà de l’équateur. C’est ce qui est généralement utilisé sur les cartes, où l’extension de longitude permet de conserver une bonne précision à peu près similaire à celle du long de l’équateur.
Une variante plus exacte de cette projection est de ne pas utiliser un cylindre parfait, mais un cylindroïde aplati aux pôles et tangent tout le long des deux méridiens opposés à l'ellipsoïde de référence.
L’intérêt de cette variante est de conserver les distances tout le long du méridien de référence. Dans ce cas aussi, la précision des distances autour des pôles ne dépend plus du méridien de référence choisi pour la projection, il devient alors possible de construire une carte rectangulaire continue couvrant la totalité des deux fuseaux opposés le long d’une fine bande (large de 6° exactement à l’équateur).
Le territoire français métropolitain est situé sur 3 fuseaux :
Europe
UTM Nord, fuseau 30 : entre 6 degrés ouest et 0 degré Greenwich ;
UTM Nord, fuseau 31 : entre 0 degré et 6 degrés est Greenwich ;
UTM Nord, fuseau 32 : entre 6 degrés est et 12 degrés est Greenwich.
Une projection ne doit pas être confondue avec un système géodésique (par exemple WGS72, WGS84, RGF93) permettant de localiser un point à la surface de la Terre. N'importe quelle projection peut être associée à n'importe quel système géodésique ; si aujourd'hui le système géodésique utilisé est généralement basé sur WGS84, il convient toutefois, pour éviter les ambiguïtés, d'associer les noms du système géodésique et de la projection ; par exemple en France le système géodésique NTF est resté jusqu'à récemment le système réglementaire et est généralement associé à la projection Lambert II étendu, mais on trouve aussi les projections Lambert Zone I à IV.
La projection UTM est associée à un point de référence virtuel tel que l'intersection de l'équateur et du méridien central de la zone considérée ait pour coordonnées :
pour l’hémisphère Nord : abscisse +500 km, ordonnée 0 ;
pour l’hémisphère Sud : abscisse +500 km, ordonnée +10 000 km.
Ce décalage de point de référence permet d’avoir des coordonnées positives pour l’intégralité des points de la zone.
Coordonnées : géographiques ou projection ?
Formules de passage de latitude,longitude (φ,λ) aux coordonnées UTM (E,N)
Formules de passage de coordonnées UTM (E,N) aux latitude,longitude (φ,λ)
Voir aussi
Références
Dernière modification il y a 11 mois par Polmars
PAGES ASSOCIÉES
Projection conique conforme de Lambert
projection cartographique
Coordonnées sphériques
système 3-dimensionel coordonnée
Quadrivecteur potentiel
Le contenu est disponible sous licence CC BY-SA 3.0 sauf mention contraire.
Ajouter un commentaire